Published on

🧰 The Role of Activation Functions in Neural Networks

Authors

🧰 The Role of Activation Functions in Neural Networks

Activation functions are the unsung heroes of deep learning. Without them, neural networks would simply be stacks of linear operations — no matter how deep. In this post, we dive into how activation functions work, why they're essential, and how to choose the right one for your model.

🔍 Why Do We Need Activation Functions?

Imagine a neural network without activation functions — it's just a big linear equation. No matter how many layers you stack, the output remains a linear function of the input.

Activation functions introduce non-linearity, enabling networks to approximate complex functions like:

  • Image recognition
  • Natural language processing
  • Reinforcement learning

Mathematically, an activation function ( f(x) ) transforms the output of each neuron before passing it to the next layer.

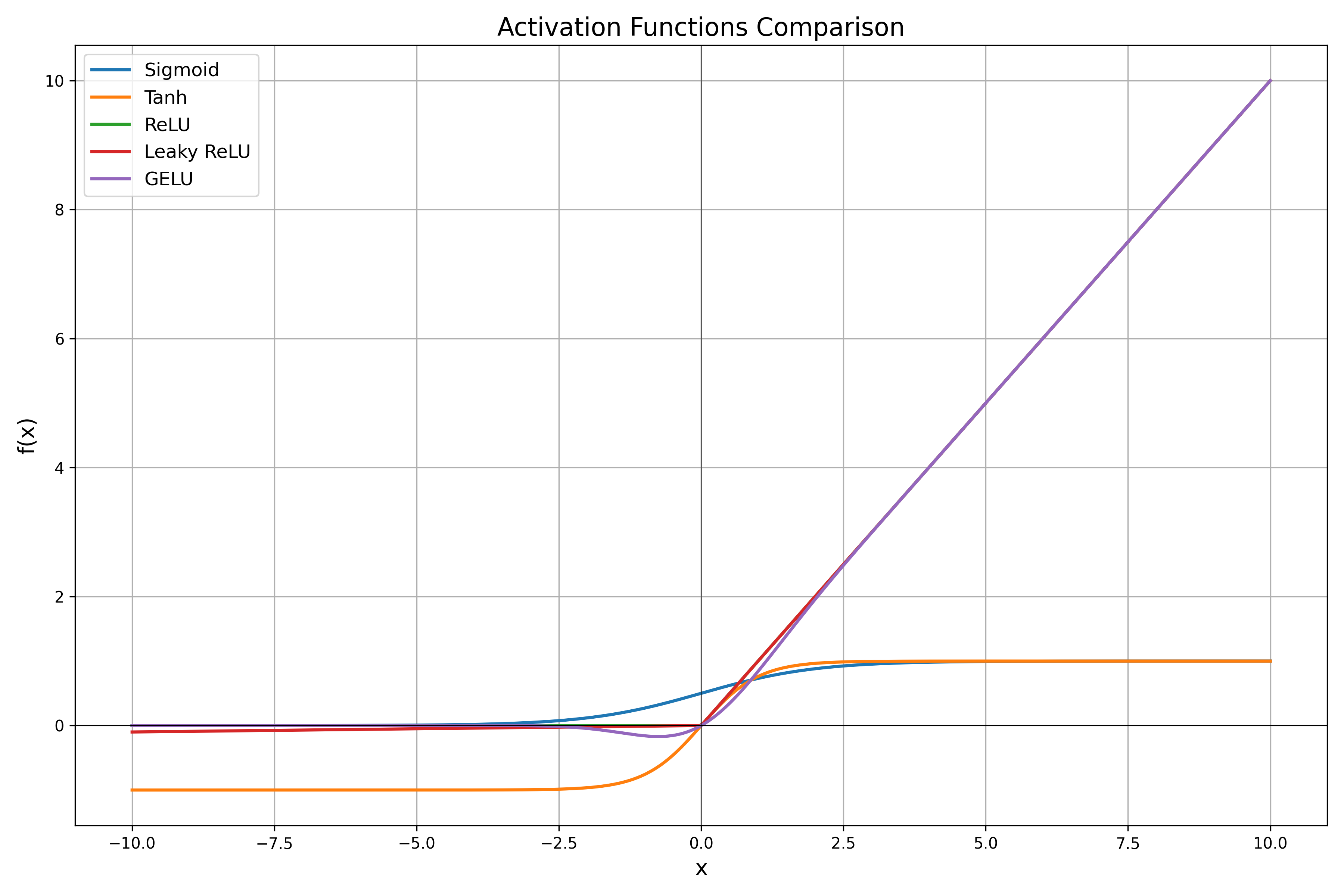
🔢 Common Activation Functions

Let's walk through the most popular activation functions, their formulas, use cases, and limitations.

1️⃣ Sigmoid

f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}
  • Range: (0, 1)
  • Use Case: Binary classification (logistic regression)
  • Drawback: Saturates for large ∣x∣|x|, causing vanishing gradients

2️⃣ Tanh

f(x)=tanh⁡(x)=ex−e−xex+e−xf(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
  • Range: (-1, 1)
  • Use Case: Often preferred over sigmoid in hidden layers
  • Drawback: Still suffers from vanishing gradients

3️⃣ ReLU (Rectified Linear Unit)

f(x)=max⁡(0,x)f(x) = \max(0, x)
  • Range: [0, ∞)
  • Use Case: Default choice for hidden layers in CNNs and MLPs
  • Advantages: Computationally efficient, sparse activation
  • Drawback: Dying ReLU problem — neurons may output zero permanently

4️⃣ Leaky ReLU

f(x)={xextifx≥0αxextifx<0f(x) = \begin{cases} x & ext{if } x \geq 0 \alpha x & ext{if } x < 0 \end{cases}
  • Fixes ReLU's dying neuron problem by allowing a small slope in the negative region (α≈0.01\alpha \approx 0.01)

5️⃣ GELU (Gaussian Error Linear Unit)

f(x)=x⋅Φ(x)f(x) = x \cdot \Phi(x)

Where Φ(x)\Phi(x) is the cumulative distribution function of the standard normal distribution.

  • Use Case: Transformers (e.g., BERT, GPT)
  • Advantage: Smooth and differentiable; works well in large LLMs---

📊 Visual Comparison of Activation Functions

Visual Comparison of Activation Functions

🙏 Acknowledgments

Special thanks to ChatGPT for enhancing this post with suggestions, formatting, and emojis.