🧠 AI Exploration: DBSCAN Explained

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a powerful clustering algorithm that groups together data points that are close to each other based on density - and separates outliers.

Unlike K-Means, you don't need to specify the number of clusters in advance.

🧠 How DBSCAN Works

DBSCAN relies on two parameters:

• eps: The maximum distance between two points to be considered neighbors
• min_samples: The minimum number of neighbors needed to form a dense region

It classifies points as:

1. Core Point: Has at least min_samples within eps radius
2. Border Point: Within eps of a core point but not a core itself
3. Noise Point: Not within eps of any core point

Clusters are formed by expanding core points, while noise points are ignored.

🧮 Mathematical Definition of DBSCAN

Let’s define a few key terms more formally:

1. ε-neighborhood of a point

Given a point $x \in \mathbb{R}^d$ and radius $\varepsilon > 0$,

This is the set of all points within distance $\varepsilon$ of $x$.

2. Core Point

A point $x$ is a core point if:

That is, it has at least minPts neighbors (including itself) in its ε-neighborhood.

3. Direct Density-Reachability

A point $x$ is directly density-reachable from a point $y$ if:

• $x \in N_{\varepsilon}(y)$
• $y$ is a core point

4. Density-Reachability

A point $x$ is density-reachable from $y$ if there exists a chain of points:

such that $x_{i+1}$ is directly density-reachable from $x_i$.

5. Density-Connected

Two points $x$ and $y$ are density-connected if there exists a point $z$ such that both $x$ and $y$ are density-reachable from $z$.

🎯 When to Use DBSCAN

• When clusters have irregular shapes (not spherical)
• When data contains outliers
• When you don’t know how many clusters exist

✅ Advantages and Disadvantages

✅ Pros

• Does not require you to specify number of clusters
• Can detect outliers (label as noise)
• Works well with clusters of arbitrary shape

❌ Cons

• Choosing eps and min_samples can be tricky
• Performance degrades in high-dimensional spaces

🧪 Code Example: DBSCAN on Iris Dataset

from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

# Load dataset
iris = load_iris()
X = iris.data
features = iris.feature_names

# Standardize features (important for distance-based models)
X_scaled = StandardScaler().fit_transform(X)

# Run DBSCAN
dbscan = DBSCAN(eps=0.6, min_samples=4)
clusters = dbscan.fit_predict(X_scaled)

# Visualize
df = pd.DataFrame(X, columns=features)
df['Cluster'] = clusters

sns.pairplot(df, hue='Cluster', palette='Set1', corner=True)
plt.suptitle('DBSCAN Clustering on Iris Dataset', y=1.02)
plt.tight_layout()
plt.show()

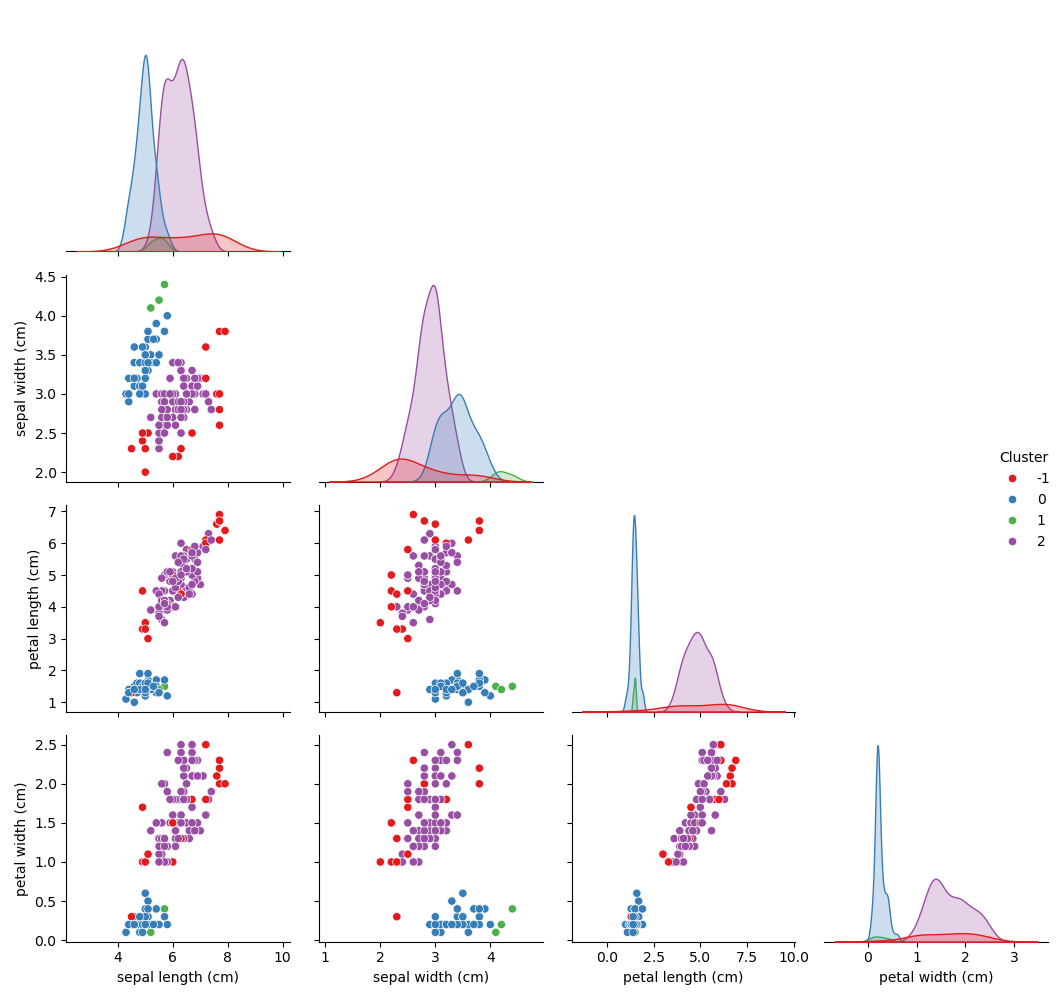
This example uses DBSCAN to automatically find structure in the Iris dataset - no cluster count needed.

📊 The plot below reveals how DBSCAN discovered three dense clusters and labeled several outlier points as noise (in red, cluster -1). Unlike K-Means, DBSCAN effectively identifies non-spherical structures and isolates sparse, scattered points - showcasing its strength in handling real-world imperfections.

🔍 K-Means vs. DBSCAN Comparison

K-Means (previous post) cleanly splits the Iris dataset into three compact, spherical clusters, assuming equal density and ignoring outliers.

DBSCAN (this post), in contrast, is density-aware - it detects clusters of varying shapes and automatically flags outliers (in red, cluster -1). This makes DBSCAN more suitable for datasets with noise or uneven cluster sizes, whereas K-Means may struggle when clusters are non-convex or imbalanced.

📊 Notes on Parameter Tuning

• Use k-distance plot to find a good value for eps
• Set min_samples roughly equal to the number of features or slightly larger

🔚 Recap

DBSCAN is ideal for clustering spatial, noisy, or arbitrarily shaped data without predefining the number of clusters. Its ability to handle noise makes it a go-to algorithm for real-world exploratory clustering tasks.

🔜 Coming Next

Next in this subseries of clustering techniques: Hierarchical Clustering - where we build a tree of nested clusters and cut it at the desired level.

Stay curious and keep exploring 👇